Fractal geometry:
- Stem To Go

- Jan 23, 2021
- 3 min read
What are fractals?
The most basic description of a fractal is a never-ending pattern. They are mathematical shapes that are infinitely complex and regardless of whether you zoom in or zoom out, the image practically looks the same.
(Below is a picture of The Mandelbrot Set (a fractal) zoomed in)

Fractals were first discovered, in essence, by Gaston Julia in 1919. He repeated a simple mathematical rule over and over and over again to observe what would happen as the repetitions kept increasing. His repetitive experiment led him to observe impressively complicated structures which, at this time, couldn’t fully be appreciated considering their lack of technology. It was many decades later, after computer generated imagery had become a fundamental in society, before these exceptionally intricate structures were given a name – fractals.
Considering Gaston Julia’s limitations – he managed to create graphical fractals in essence using complex numbers (a number in the form a + bi where ‘a’ is real integer and ‘bi’ is an imaginary component) – this was known as a Julia set.
Julia sets and The Mandelbrot set (one of the first shapes to be recognised as a fractal) are both based upon the same idea – where you choose two complex numbers Z and C and then repeatedly evaluate:
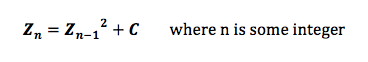
The Mandelbrot Set is actually a two-dimensional subset of this repeated evaluation (whereby you always set Zn = 0 and thus, just vary C). If you were to vary then this fractal actually spans four dimensions however that proves rather impossible to visualise.
Similarly, a Julia Sets incorporates the same idea (with complex number K, you always set C = K and vary Zo) however, Julia Sets only span a maximum of two dimensions, unlike The Mandelbrot Set.
In general, Julia sets have less variation than The Mandelbrot Set however, The Mandelbrot Set can be considered to be a representation of all possible Julia Sets as it varies C at each location.
Via this links, you can zoom in on The Mandelbrot Set –
Fractals in nature:
Fractals are not only limited to maths however – fractals are actually a naturally occurring pattern in nature!
Some examples of fractals in nature includes; the intricate pattern and structure of snowflakes, fractals in plants (normally seen in the repetitive arrangement of their petals or leaves).
Fractals can also been seen in trees – where the trunk is the main frame and then you have branches that grow outwards, and then you have smaller branches that grow on these branches, and then even smaller branches that grow on those branches etc.
I think, however, the most interesting types of naturally occurring fractals are those of the respiratory and circulatory system inside ourselves and other animals. You can see these fractals in the bronchi insides our lungs (where you have a primary bronchi, which stems into a secondary bronchi, which stems into a tertiary bronchi, which stems into bronchioles etc – making a beautiful fractal pattern). You can also see a naturally occurring fractal pattern in the circulatory system where arteries that stem into capillaries etc.
Fractals even occur in geographical landforms such as mountains and lakes!
References:
“The Mandelbrot Set and Julia Sets.” The Mandelbrot Set and Julia Sets, www.alunw.freeuk.com/mandelbrotroom.html. Accessed 19 Jan. 2021.
John. “What Is a Fractal? - The Ultimate Guide to Understanding Fractals.” Iternal Technologies, 24 Sept. 2020, iternal.us/what-is-a-fractal.
“What Are Fractals? – Fractal Foundation.” What Are Fractals? - Fractal Foundation, fractalfoundation.org/resources/what-are-fractals. Accessed 19 Jan. 2021.
Photo credits:
“Mandelbrot Viewer.” Mandelbrot Viewer, math.hws.edu/eck/js/mandelbrot/MB.html. Accessed 19 Jan. 2021.



Comments