What is hyperbolic geometry?
- Stem To Go

- Feb 6, 2021
- 3 min read
Updated: Feb 7, 2021
Euclid’s five postulates:
As discussed in a previous article, Euclid’s Elements were a series of books that played an absolute pivotal role in the teaching of geometry for over 2000 years. At the basis of Euclid’s elements were where “Euclid’s postulates”, which are five fundamental geometric laws: the foundation on which Euclidean Geometry is built upon.
These five postulates are:
1. A straight line segment may be drawn from any given point to any other.
2. A straight line may be extended to any finite length.
3. A circle may be described with any given point as its center and any distance as its radius.
4. All right angles are congruent.
5. If a straight line intersects two other straight lines, and so makes the two interior angles on one side of it together less than two right angles, then the other straight lines will meet at a point if extended far enough on the side on which the angles are less than two right angles.
The fifth postulate is famously known as Euclid’s parallel postulate and is the only postulate that has never been proven (not from lack of trying). However, it was through the discovery of hyperbolic geometry in the 19th century that the status of the parallel postulate was resolved.
Hyperbolic geometry (a form of non-Euclidean geometry) is a form of geometry that satisfies all of the other four postulates except that of the Euclid’s fifth postulate (the parallel postulate).
So what is hyperbolic geometry?
Unlike the Euclidean plane (which is flat), the hyperbolic plane is fundamentally curved – it has in fact been shown that hyperbolic surfaces have a constant negative curvature. Another notable feature of hyperbolic surfaces is that, as a consequence, three angles which make up a triangle will add up to less than 180 degrees (a fact that goes against a fundamental of Euclidean geometry). A picture of a hyperbolic surface is shown below.
Figure 1

There are in fact three models of hyperbolic geometry. Though they suffer from distortion, these can be viewed as projections of the hyperbolic surface. These three models are:
- The Klein-Beltrami model (the first complete model and the first to be labelled as ‘hyperbolic’)
- The Poincaré disk model
- The Poincaré upper half-plane model
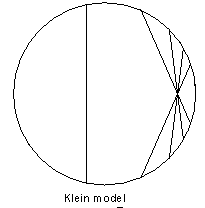
The Klein-Beltrami model (shown in the diagram below) involves mapping a hyperbolic surface onto the interior of a circle. This model preserves straightness by including geodesics corresponding to particular chords within the circle. This, however, causes angles to become distorted (hence why the angles in a triangle will add up to less than 180 degrees).
Figure 2
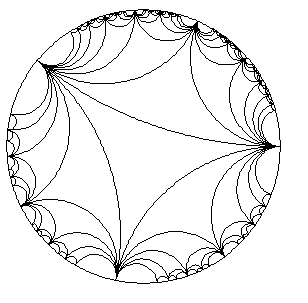
The Poincaré disk model (shown in the diagram below) is similar to the Klein-Beltrami model in the fact that the hyperbolic surface is mapped onto the interior of a circle. Similarly, geodesics are again used. However, they are now used to map diameters and circular arcs (not chords) within the circle which are perpendicular to the edge of the circle. Unlike the Klein-Beltrami model, the Poincaré disk model distorts distances but not angles.
Figure 3
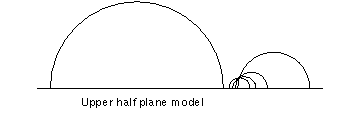
The Poincaré upper half-plane model (shown in the diagram below), unlike the two above models, involves mapping a hyperbolic surface onto a half-plane above the x-axis. Geodesics are once again used to map vertical lines that are perpendicular to the x-axis. Similarly to the Poincaré disk model, the Poincaré upper half-plane model also distorts distances but not angles.
Figure 4
References:
Henderson, David. “Non-Euclidean Geometry | Definition & Types.” Encyclopedia Britannica, www.britannica.com/science/non-Euclidean-geometry#ref828724. Accessed 4 Feb. 2021.
Picture references:
Figure 1:
“Hyperbolic Surfaces.” Hyperbolic Surfaces, www.math.wisc.edu/%7Emeyer/airsculpt/sculpt07.html. Accessed 4 Feb. 2021.
Figure 2, and 4:
“Models of the Hyperbolic Plane.” Models of the Hyperbolic Plane, www.geom.uiuc.edu/docs/forum/hype/model.html. Accessed 4 Feb. 2021.
Figure 3:
“Poincaré Hyperbolic Disk -- from Wolfram MathWorld.” Ponicaré Hyperbolic Disk, mathworld.wolfram.com/PoincareHyperbolicDisk.html. Accessed 4 Feb. 2021.



Comments